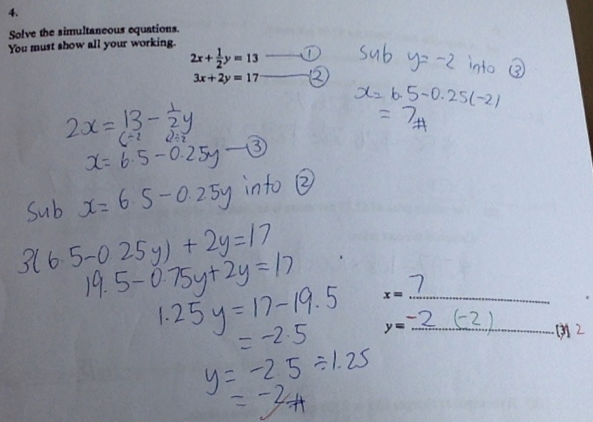CHAPTER 1: NUMBER

Real numbers: A number that lies on the number line

Natural numbers: used for counting purposes

Whole numbers: Natural numbers including 0

Integer: Both positive and negative whole number

Prime number: A number divisible only by itself and one (Note: 1 is not a prime number)

Cube number: A rational number multiplied by itself three times

Common factors: Common divisers of a number

Common multiples: Multiples of two or more numbers that are the same.

Surds: Numbers that cannot be squared/evaluated properly.

Rational numbers: can be written as a fraction

Irrational numbers: cannot be written as a fraction

Finding the nth term

Linear Sequence

The n^th term of a sequence is always written in the form an + b

where a = the difference to get from one term to the next and b = (first term – a)

e.g. 6, 11, 16, 21, …For this sequence a = 5, b = 6 – 5

So the formula is nth term = 5n + 1

Quadratic sequences

Where a pattern in the members of a sequence is in the second level difference between the terms.

General equation: 𝑎𝑛² + 𝑏𝑛 + 𝑐

Cubic sequences

Where a pattern in the members of a sequence is in the third level difference between the terms.

General equation: 𝑎𝑛³ + 𝑏𝑛² + 𝑐𝑛 + d

Approximation and Estimation

Significant Figures Rules

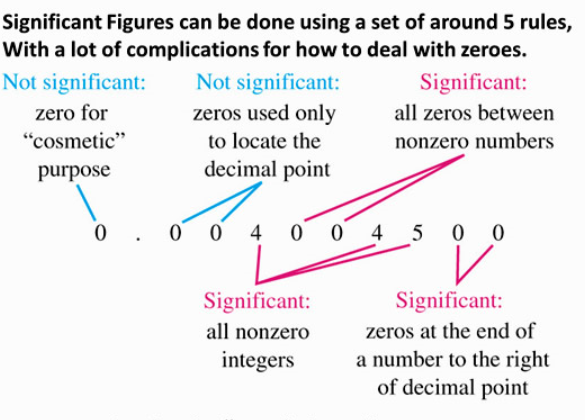
Upper and lower bounds

• Given the accuracy to which a figure is given to, the original value which the arrived value is reached can be found.
• If 5.4 to correct to 2 d.p, the original number could be anywhere between 5.35 to 5.45. Therefore:
• Upper Bound of 5.4= 5.45
• Lower Bound of 5.4= 5.35

Standard Form

Any number can be expressed in standard form if written in this format:

𝐴 × 10ⁿ 𝑠𝑢𝑐ℎ 𝑡ℎ𝑎𝑡 1 ≤ 𝑛 < 10

for example,

Ratios and Proportions

Ratios are used to show how things are shared and can be fully simplified just like fractions.

For example, the necklace in the image has a pattern of two red beads for every three yellow beads as 6: 9 = 2:3

Currency Exchange

New Exchanged Amount = amount x (New rate/Old rate)

Map Scales

Using proportion to work out map scales

1km = 1000m 1m = 100cm 1cm = 10mm

Some scales are given as ratios and are displayed like this 1:500. This means that each centimetre as measured is equal to 500 cm in real life. A scale of 1:20 000 would mean that 1 cm is actually equivalent to 200 m.

For Example:

Percentages

A percentage is a proportion that shows a number as parts per hundred, one way of expressing numbers that are part of a whole. It can also be written as fractions or decimals. 50% can also be written as a fraction, or a decimal, 0.5. They are all exactly the same amount.

Percentage Increase and Decrease

[(New value –  Original value)/ Original Value] x 100

Simple interest:
𝐼 = 𝑃𝑅𝑇/ 100
𝑃 = 𝑃𝑟𝑖𝑛𝑐𝑖𝑝𝑎𝑙, 𝑅 = 𝑅𝑎𝑡𝑒 𝑜𝑓 𝐼𝑛𝑡𝑒𝑟𝑒𝑠𝑡 (𝑎𝑠 𝑎 𝑛𝑢𝑚𝑏𝑒𝑟), 𝑇 = 𝑃𝑒𝑟𝑖𝑜𝑑 𝑜𝑓 𝑇𝑖𝑚𝑒

Compound interest:

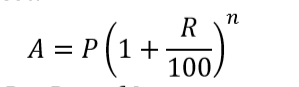
𝑃 = 𝑃𝑟𝑖𝑛𝑐𝑖𝑝𝑎𝑙, 𝑅 = 𝑅𝑎𝑡𝑒 𝑜𝑓 𝐼𝑛𝑡𝑒𝑟𝑒𝑠𝑡 as a number, 𝑛 = 𝑃𝑒𝑟𝑖𝑜𝑑 𝑜𝑓 𝑇𝑖𝑚𝑒

Speed, Distance & Time

Units of speed: km/hr, m/s

Units of distance: km /m

Units of time: hr/ sec

Algebra

Factorisation

Common factors:
3a² + 6a

3a(a + 2)

Difference of two squares:

25 − a² 

(5 + a)(5 − a)

Group factorization:

4𝑑 + 𝑎𝑐 + 𝑎𝑑 + 4𝑐

4(𝑑 + 𝑐) + 𝑎(𝑐 + 𝑑)

Trinomial:

𝑥² + 14𝑥 + 24
𝑥² + 12𝑥 + 2𝑥 + 24

𝑥(𝑥 + 12) + 2(𝑥 + 12)

(𝑥 + 2)(𝑥 + 12)

Full square:

𝑥² + 2𝑥𝑦 + 𝑦²
𝑥² + 𝑥𝑦 + 𝑥𝑦 + 𝑦²

𝑥(𝑥 + 𝑦) + 𝑦(𝑥 + 𝑦)

(𝑥 + 𝑦)(𝑥 + 𝑦)

(𝑥 + 𝑦)²

Simultaneous Equations

Simultaneous linear equations can be solved either by substitution or elimination

Substitution

Step 1: obtain an equation in one unknown and solve this equation

Step 2: substitute the results from step 1 into the linear equation to find the other unknown

Elimination:

𝟐𝒂 + 𝒃 = 𝟏𝟎

𝟐𝒃 + 𝒂 = 𝟏𝟏

2𝑎 + 𝑏 = 10

2(𝑎 + 2𝑏) = 11(2)

2𝑎 + 𝑏 = 10

2𝑎 + 4𝑏 = 22

2𝑎 + 𝑏 − (2𝑎 + 4𝑏) = 10 − 22

𝑏 = 4

2𝑎 + 4 = 10

∴ 𝑎 = 3

Note: A solution to a system of two linear equations may be interpreted graphically as a point of intersection between the two line

Quadratic Equations

Nature of Roots

b^2 −4ac > 0 ⇔ two real and different roots

b^2 −4ac = 0 ⇔ two real and equal roots

b^2 −4ac < 0 ⇔ no real roots

b^2 −4ac ≥ 0 ⇔ the roots are real

Variation

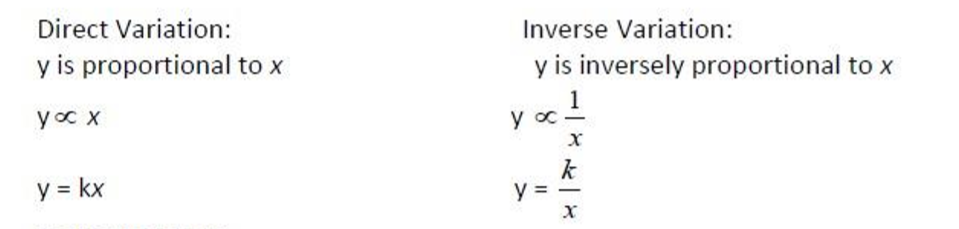
Indices

Inequalities

• Solve like equation

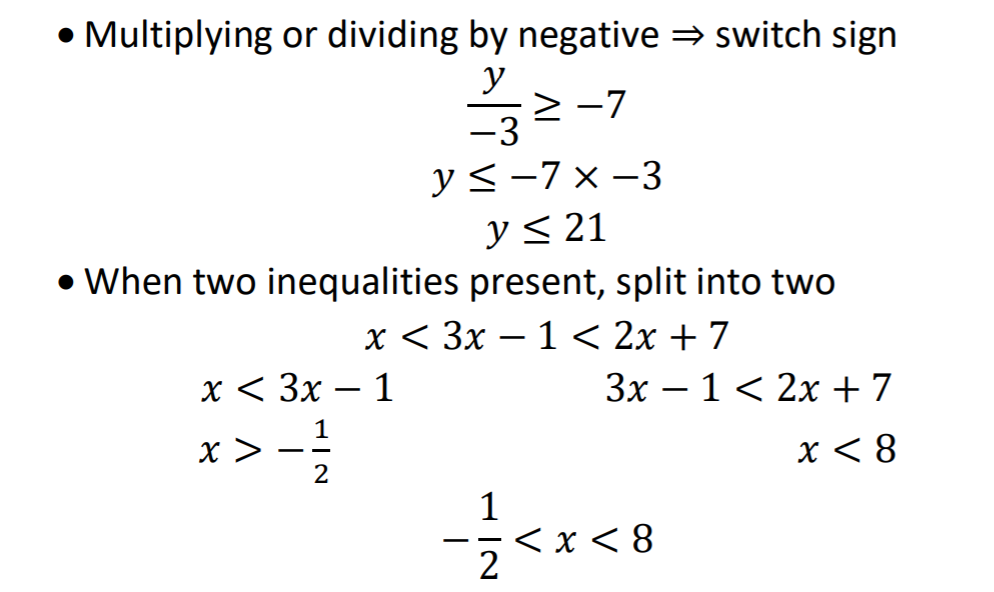
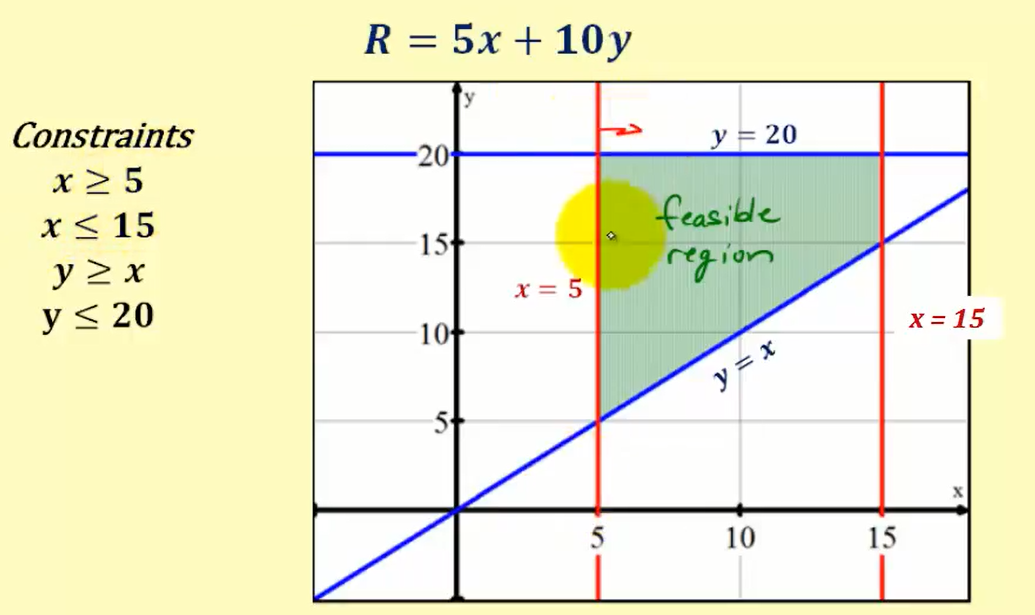
Linear Programming

• Use broken line for (<,>)
• Use solid line for (≤,≥)
• Express in the form 𝑦 = 𝑚𝑥 + 𝑐
  • Draw straight line graphs
  • Shade the wanted/unwanted region
  • after all the inequalities are plotted, the shaded/unshaded region will be the solution
• For example:

Mensuration

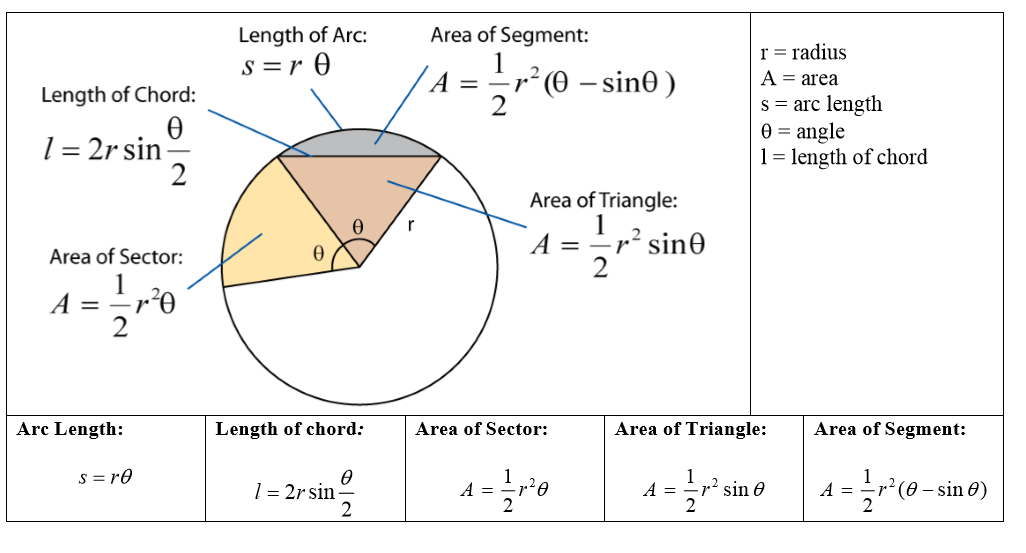
Circle Theorem

Geometry

Pythagoras Theoram:

For all the right angled triangles “the square on the hypotenuse (c²) is equal to the sum of all the squares on the other two sides (a² + b² ).

c² = a² + b²

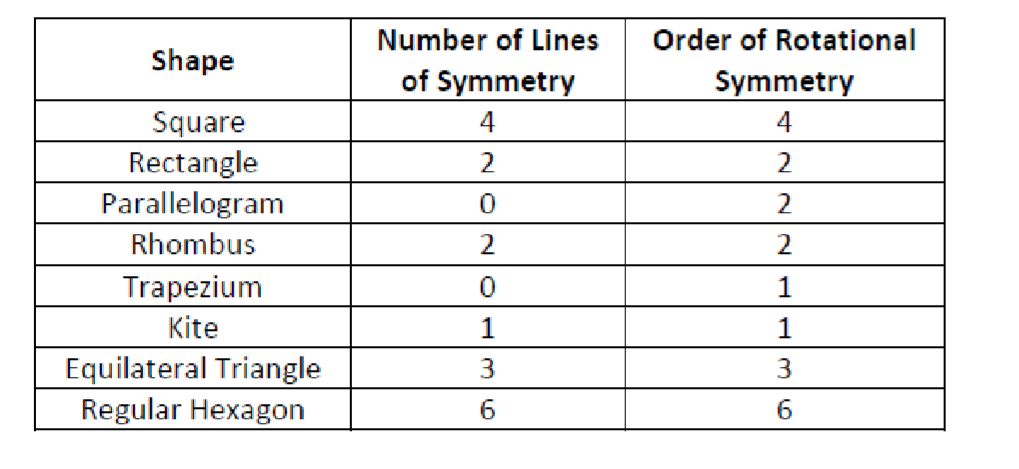
Symmetry

A line of symmetry divides a two-dimensional shape into two congruent (identical)

A plane of symmetry divides a three-dimensional shape into two congruent solid shapes.

The number of times shape fits its outline during a complete revolution is called the order of rotational symmetry.

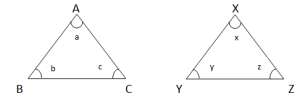
Congurency:

Two geometric figures are congurent, if they are of the same shape and size.

AB =XY               ∠a = ∠x

BC = YZ               ∠b = ∠y

AC = XZ               ∠c = ∠z

Tests of Congurency:

• Side Side Side (SSS) – all sides are equal
• Angle Angle Angle (AAA) – all angles are same
• Side Angle Side (SAS) – two sides and one angle are equal
• Right Angled – Hypotenuse – Side – one right angle and hyp & side equal

≡  – To denote “ is congruent to”

≢ – To denote “ is not congruent to”

Similarity:

When two figures are similar, they are exactl the same in shape but not in size.

Test:

• Equal corresponding Angles:

The angles of one triangle are equal to corresponding angles of the other triangle.

• Proportional Corresponding Angles.
• Two Pairs of Proportional Corresponding Sides with equal angles.

We right similarity as ( ~ ) i.e ΔABC ~ ΔDEF

Ratios of Area And Volumes:

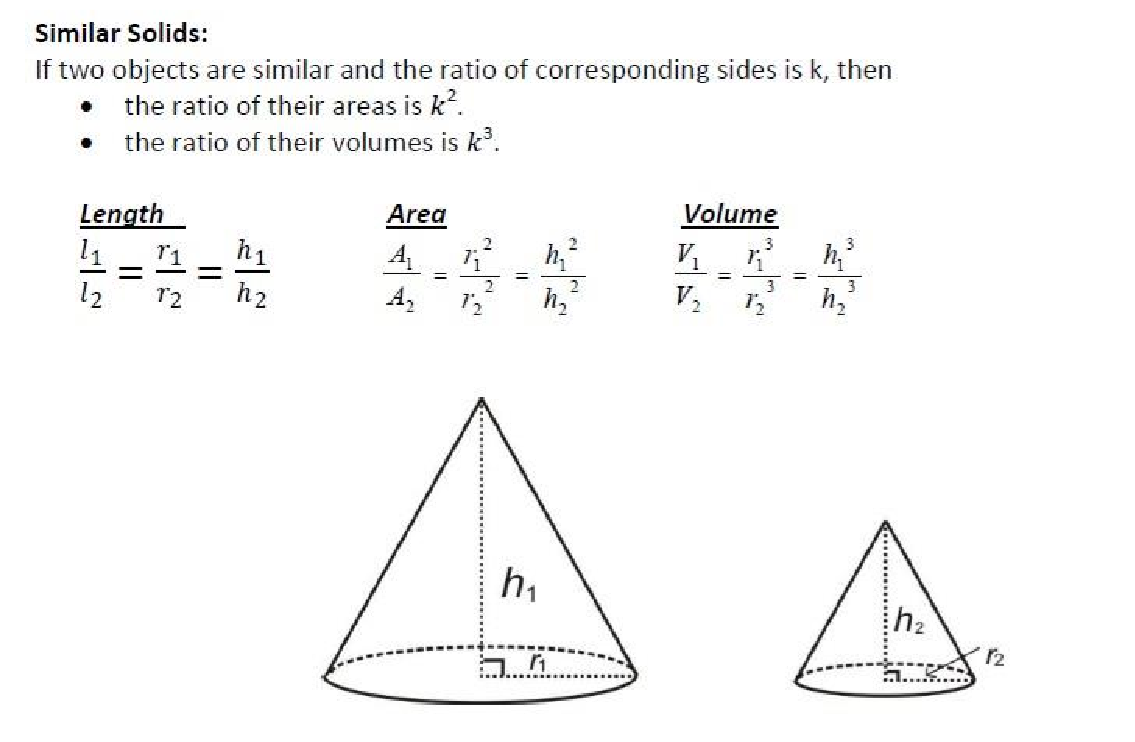
Trigonometry

Trigonometrical Ratios of Acute Angle:

All angles in a right angle triangle are acute angles. (between 0 to 90 degrees).

Sine:

Cosine:

Tangent:

Tip to remember this SOH CAH TOA.

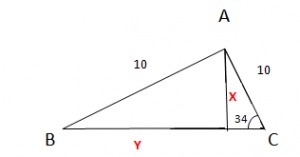
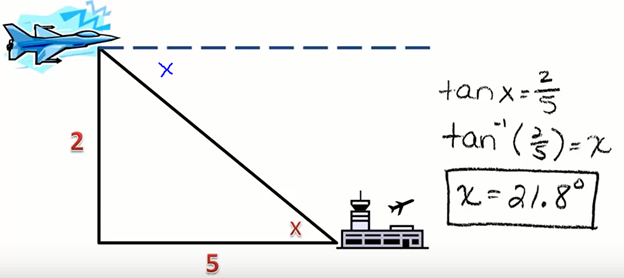
Example:

Q: Find the unknown values of :

           Sin 30 = Opposite / Hypotenuse

Sin 30 = x / 13

X = 6.5 Ans

Y² + X² = 10²

Y² = 10² –  6.5²

Y = 7.60 (Ans)

Trigonometrical Ratios of Obtuse Angles:

The trigonometric ratios of an obtuse angle (between 90 and 180 degree) can be expressed in terms of the adjacent acute angle that lies in the same straight line.

Area of Triangle:

For a known right angled triangle with any two sides given and the area.

 Area = ½ ab sin C

Area = ½ bc sin A

Area = ½ ac sin B

Sine Rule:                

It can be used when:

• Two angles and one side given.
• Two sides and one non-included angle given.

Cosine Rule:

a²⁼ b² = c² – (2bc cos A)

b²⁼ a² = c² – (2ac cos B)

c²⁼ a² = b² – (2ab cos C)

It can be used when:

• Three sides are given.
• Two sides and one angle is given.

Bearing

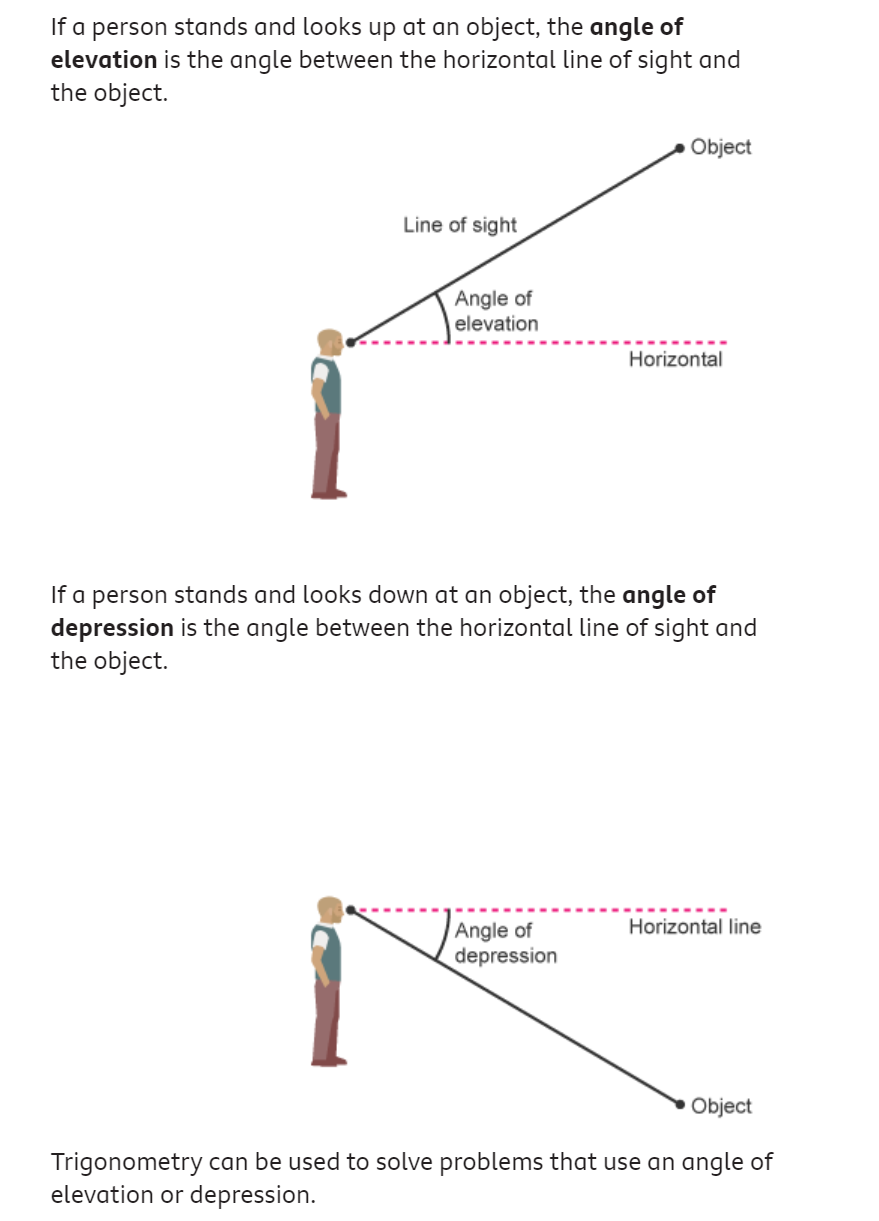
Angles of elevation and depression

Three-dimensional problems

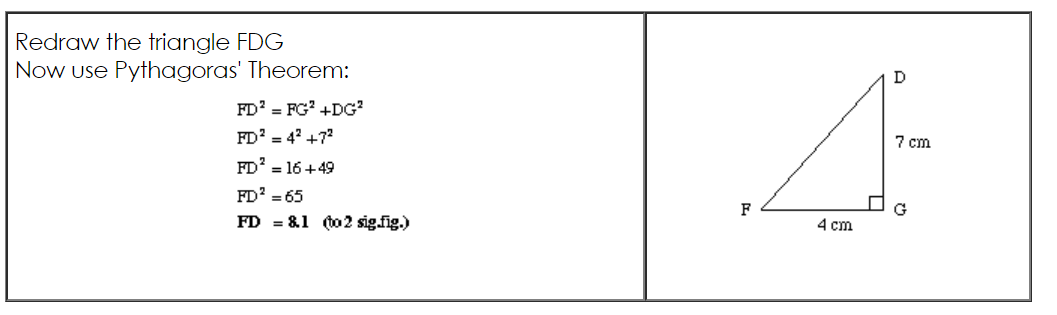
When a three-dimensional problem has to be solved, the best way is to try and isolate and redraw the triangles involved.

To find the length of FD

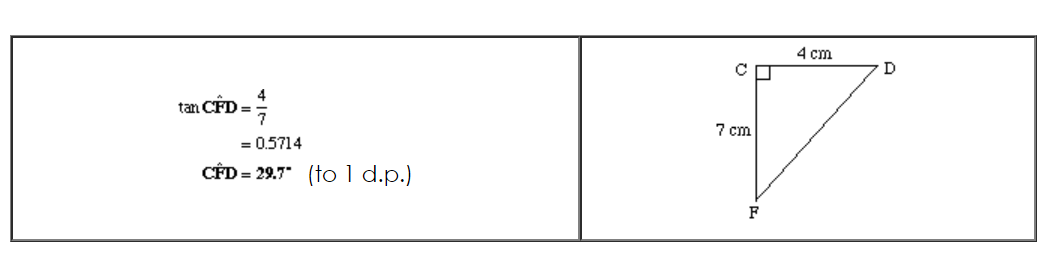
To find angle CFD

Redraw the triangle CFD
Now use SOH/CAH/TOA

GRAPHS

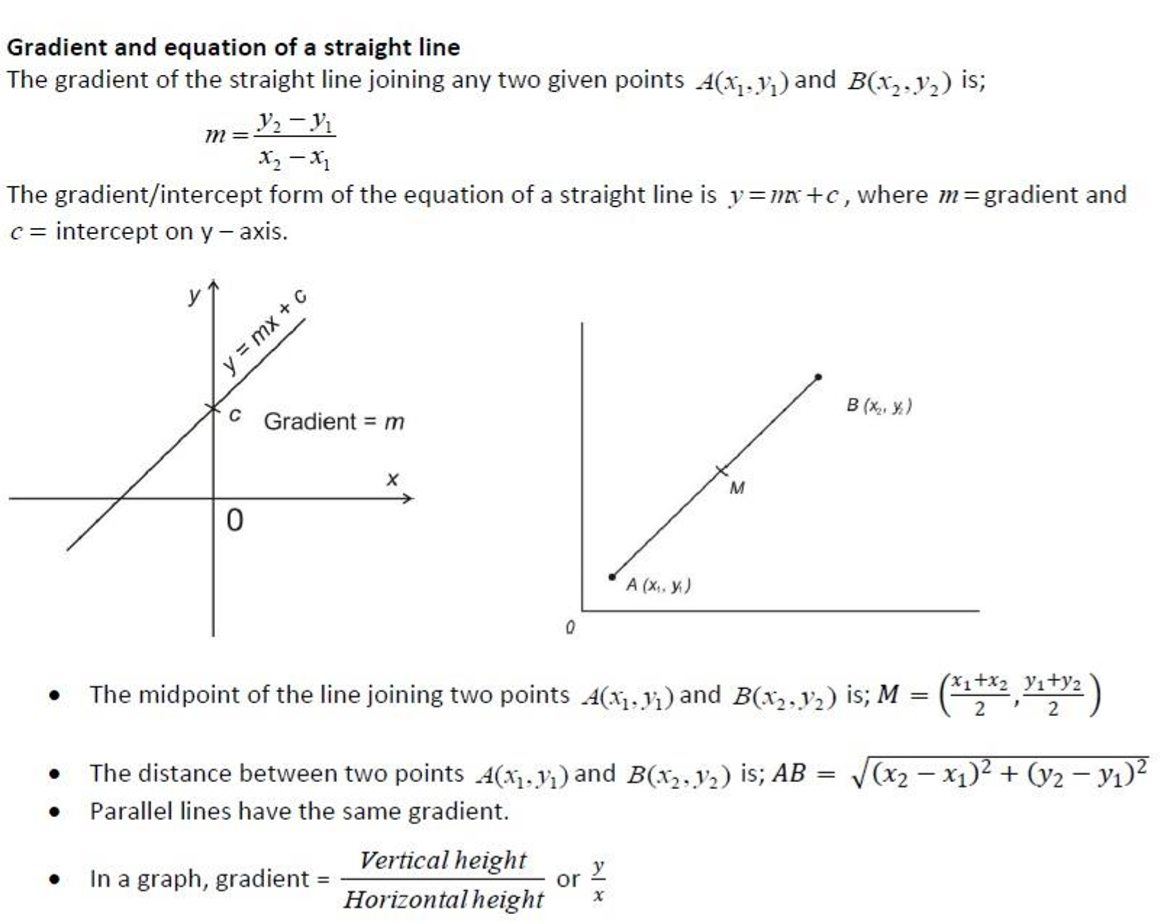
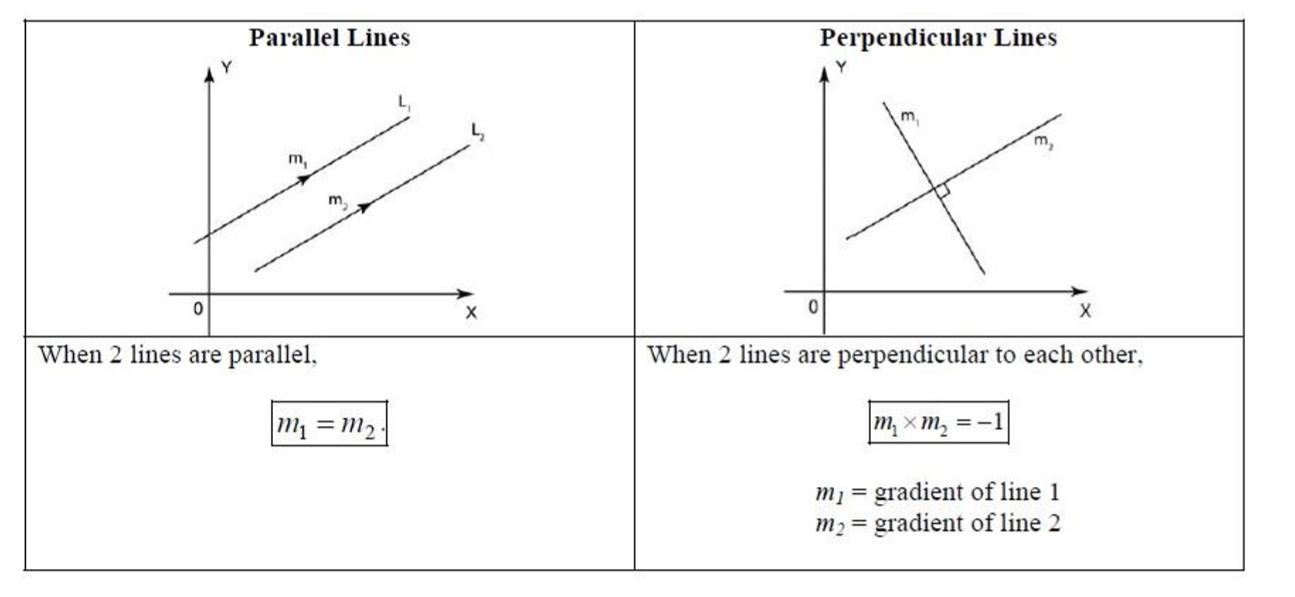
Gradient of Curve

To find the gradient of a curve, you must draw an accurate sketch of the curve. At the point where you need to know the gradient, draw a tangent to the curve. A tangent is a straight line which touches the curve at one point only. You then find the gradient of this tangent.

Example

Find the gradient of the curve y = x² at the point (3, 9).

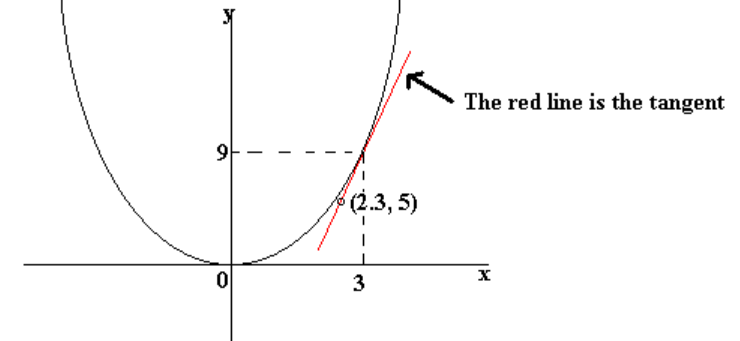
Gradient of tangent = (change in y)/(change in x)
= (9 – 5)/ (3 – 2.3)
= 5.71

Sketching Graph

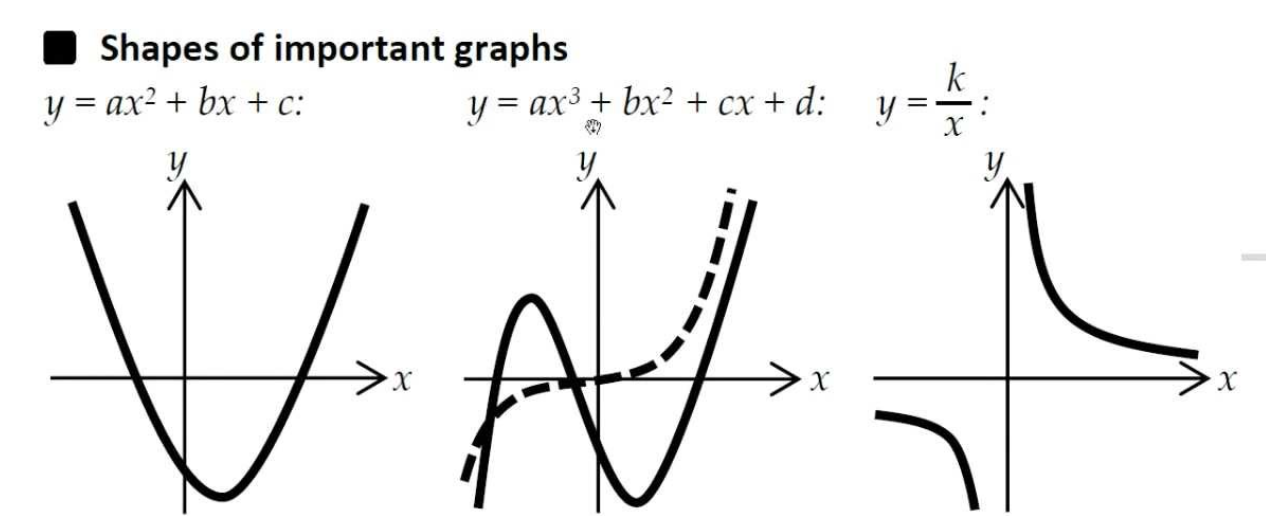
Graphical Solution of Equations

If we are given any quadratic graph:   y = ax² + bx + c

We can solve any quadratic equation:              Ax² + Bx + C = 0

             by drawing only a straight line

             We begin with:                                       Ax² + Bx + C = 0

             Divide by A and multiply by a, we get:

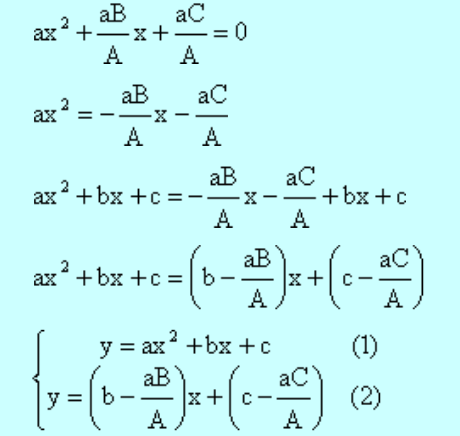
(1)   is the given quadratic graph and (2) is the straight line graph you need to draw.

             The intersection(s) of these two graphs is/are the root(s) of the equation: 

                                             Ax² + Bx + C = 0.

             Note:     If there is no intersection point, the equation: Ax² + Bx + C = 0

                             has no real roots.

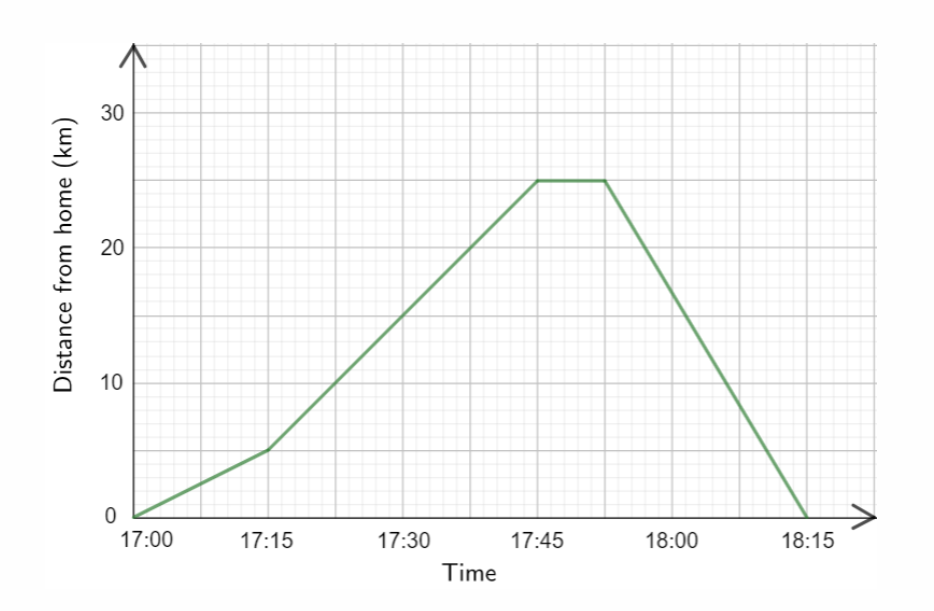
Distance-time graph

The gradient of a distance-time graph represents the speed.

For example:

Between 17:15 and 17:45:

Gradient = (25-5)/0.5​=40km/h

Speed-time graph

The gradient of a speed-time graph represents the acceleration. The area between the curve and the x axis of a speed–time graph represents the distance travelled.

For example:

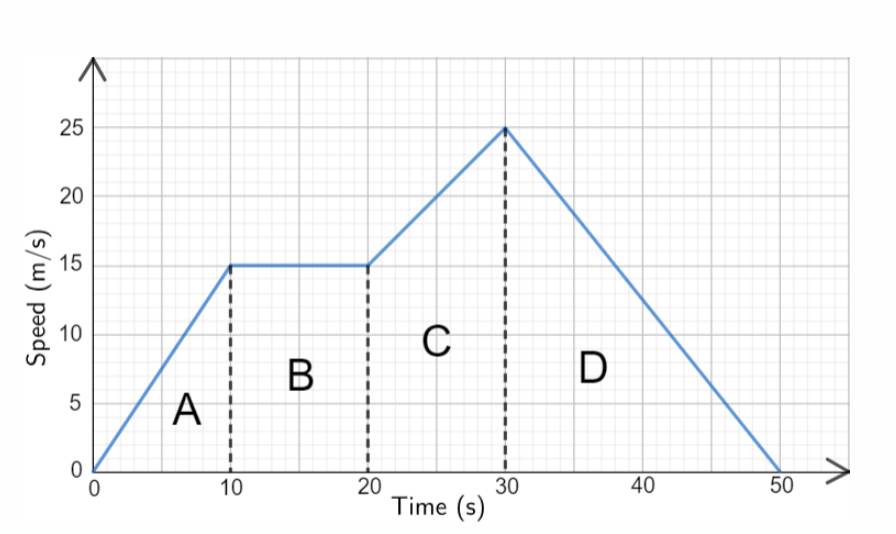
Distance travelled = Sum of areas A, B, C and D

= 75+150+200+250=675m

Maximum acceleration occurs from 0 to 10s

gradient= (15-0)/(10−0)​=1.5m/s²

DISCLAIMER: The content displayed below contains a plethora of mistakes, which can trigger serious symptoms like fainting, eye cancer, and in the worst case death if exposed for long periods of time to the naked eye. The creator of this blog will NOT be held accountable for any damages caused. Enjoy!

QUESTION 1:

Reflection: It is about time that I stop being that careless.Time to wake up before it is too late.

QUESTION 2:

Reflection: Don’t overcomplicate things. I had obviously worked out the answer, but I continued working on the question…

QUESTION 3:

Reflection: ALWAYS factorise the variable ‘a’ before completing the square. For example, if ‘a’ is greater than or smaller than 1, factor it outside the brackets before completing the square. 

QUESTION 4:

Reflection: This is pretty much self-explanatory. Go see for yourselves. 

BONUS QUESTION

Reflection: Just exercise better time management. DO NOT spend more than 3 minutes per question or face grave consequences.

Hope you enjoyed reading this! If you had, please kindly share the link in the description below:

https://wordpress.com/block-editor/post/mathsoverload.home.blog/75

“The description of right lines and circles, upon which geometry is founded, belongs to mechanics. Geometry does not teach us to draw these lines, but requires them to be drawn.”

Isaac Newton

Isaac Newton

Introduction to Geometry and Trigonometry:

Geometry is everywhere. Angles, shapes, lines, line segments, curves, and other aspects of geometry are every single place you look. Trigonometry is a subset of mathematics that studies relationships between the sides and angles of triangles. Trigonometry is found all throughout geometry, as every straight-sided shape may be broken into as a collection of triangles. Sine, cosine and tangent are the principle trigonometric functions.

Source: https://www.youtube.com/watch?v=qXxTu0fg4_8

Source: http://www.departments.bucknell.edu/history/carnegie/building/blueprint.html

In conclusion, it is evident that both trigonometry and geometry play very important roles in our lives, and we would not have achieved what the world was like today without them.